「分层图」

Author Avatar
落影汐雾 9月 23, 2019
  • 在其它设备中阅读本文章

Update on A.D.2019-09-23

问题

在一个无向图$G=(V,E)$中，可以改变$k$条边的权值为$\Delta w$，求单源最短路径。

分层图

分层图的想法就是如果有$k$条边权值变为$\Delta w$，就建$k+1$层图。

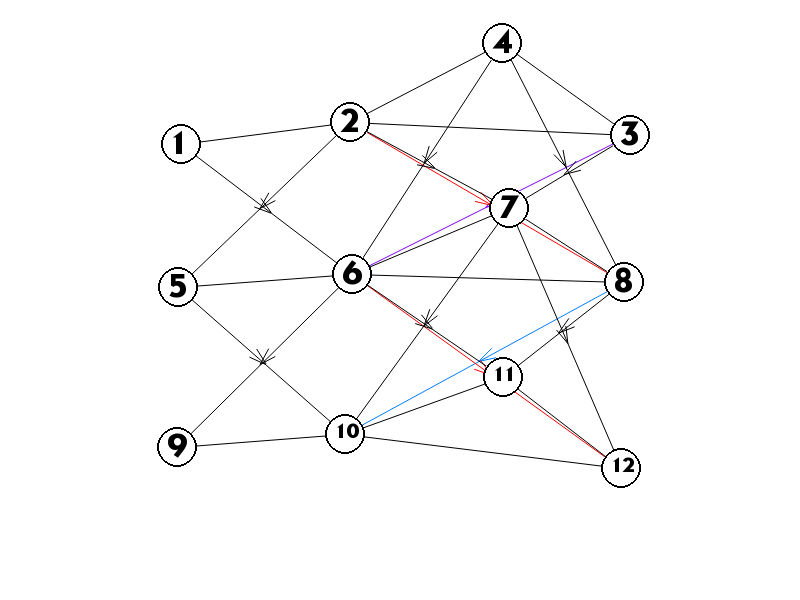
这个图实际上是这样的，对于每$1$层中相连的点对$(u,v)$连权值为$w$的无向边，对于每个在原图中相连的点对$(u,v)$由$k$层点$uk$向$k+1$层点$v{k+1}$以及$k$层点$vk$向$k+1$层点$u{k+1}$连权值为$\Delta w$的有向边，方向是从$k$层向$k+1$层。
这样构造完成一张分层图后，从第$1$层的起始点$s1$求单源最短路径，最终第$k + 1$层的终点$t{k+1}$的单源最短路径值即为答案所求。
原理其实很简单，如果从$k$层图到$k+1$层图，有向边$(uk,v{k+1})$是一条$\Delta w$权边，走这条边，相当于把$w$权边变成了$\Delta w$权边，并且进入了$k+1$层。这样如果有$k+1$层图的话，相当于进行了$k$次这种操作，自然就在$k+1$层图求最短路中实现了$k$次改变边权的目标。

题目

P2939 [USACO09FEB]改造路Revamping Trails

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;
const int N = 1e4 + 5, M = 5e4 + 5, K = 105;
int n, m, k;
struct Edge {
    int Next, to, dis;
}e[M * K * 2];
int head[N * K], num;
void add(int from, int to, int dis)
{
    e[++num].Next = head[from];
    e[num].to = to;
    e[num].dis = dis;
    head[from] = num;
}
int dist[N * K], vis[N * K];
struct node {
    int u, d;
    bool operator < (const node &x) const {
        return d > x.d;
    }
};
priority_queue<node> q;
void dijk()
{
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    q.push((node){1, 0});
    while(!q.empty())
    {
        int u = q.top().u; q.pop();
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i = head[u]; i; i = e[i].Next)
        {
            int v = e[i].to, w = e[i].dis;
            if(dist[v] > dist[u] + w)
            {
                dist[v] = dist[u] + w;
                if(!vis[v]) q.push((node){v, dist[v]});
            }
        }
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 1, u, v, z; i <= m; i++)
    {
        scanf("%d%d%d", &u, &v, &z);
        add(u, v, z); add(v, u, z);
        for(int j = 1; j <= k; j++)
        {
            add(j * n + u, j * n + v, z);
            add(j * n + v, j * n + u, z);
            add((j - 1) * n + u, j * n + v, 0);
            add((j - 1) * n + v, j * n + u, 0);
        }
    }
    dijk();
    int ans = 0x3fffffff;
    for(int i = 1; i <= k + 1; i++)
        ans = min(dist[i * n], ans);
    printf("%d\n", ans);
    return 0;
}

P4568 [JLOI2011]飞行路线

#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>

using namespace std;
const int N = 1e4 + 5, M = 5e4 + 5, K = 12;
int n, m, k;
int s, t;
struct _edge {
    int Next, v, w;
}e[M * K * 4 + M * 2];
int head[N * K], num;
void add(int from, int to, int dis)
{
    e[++num].Next = head[from];
    e[num].v = to;
    e[num].w = dis;
    head[from] = num;
}
int dist[N * K], vis[N * K];
struct node {
    int u, d;
    bool operator < (const node &x) const {
        return d > x.d;
    }
};
priority_queue<node> q;
void dijk(int x)
{
    memset(dist, 0x3f, sizeof(dist));
    dist[x] = 0;
    q.push((node){x, 0});
    while(!q.empty())
    {
        node tp = q.top(); q.pop();
        int u = tp.u;
        if(u == t + k * n) break;
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i = head[u]; i; i = e[i].Next)
        {
            int v = e[i].v, w = e[i].w;
            if(dist[v] > dist[u] + w)
            {
                dist[v] = dist[u] + w;
                if(!vis[v]) q.push((node){v, dist[v]});
            }
        }
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    scanf("%d%d", &s, &t); s++, t++;
    for(int i = 1, u, v, z; i <= m; i++)
    {
        scanf("%d%d%d", &u, &v, &z); u++, v++;
        add(u, v, z); add(v, u, z);
        for(int j = 1; j <= k; j++)
        {
            add(j * n + u, j * n + v, z);
            add(j * n + v, j * n + u, z);
            add((j - 1) * n + u, j * n + v, 0);
            add((j - 1) * n + v, j * n + u, 0);
        }
    }
    dijk(s);
    int ans = 1e9;
    for(int i = 0; i <= k; i++)
        ans = min(ans, dist[t + i * n]);
    printf("%d\n", ans);
    return 0;
}

P4822 [BJWC2012]冻结

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;
const int N = 55, M = 1005, K = 55;
int n, m, k;
struct Edge {
    int Next, to, dis;
}e[M * K * 10];
int head[N * K * 10], num;
void add(int from, int to, int dis)
{
    e[++num].Next = head[from];
    e[num].to = to;
    e[num].dis = dis;
    head[from] = num;
}
struct node {
    int u, d;
    bool operator < (const node& x) const {
        return d > x.d;
    } 
};
priority_queue<node> q;
int dist[N * K * 10], vis[N * K * 10];
void dijk()
{
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    q.push((node){1, 0});
    while(!q.empty())
    {
        int u = q.top().u; q.pop();
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i = head[u]; i; i = e[i].Next)
        {
            int v = e[i].to, w = e[i].dis;
            if(dist[v] > dist[u] + w)
            {
                dist[v] = dist[u] + w;
                if(!vis[v]) q.push((node){v, dist[v]});
            }
        }
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 1, u, v, z; i <= m; i++)
    {
        scanf("%d%d%d", &u, &v, &z);
        add(u, v, z); add(v, u, z);
        for(int j = 1; j <= k; j++)
        {
            add(j * n + u, j * n + v, z);
            add(j * n + v, j * n + u, z);
            add((j - 1) * n + u, j * n + v, z >> 1);
            add((j - 1) * n + v, j * n + u, z >> 1);
        }
    }
    dijk();
    int ans = 0x7fffffff;
    for(int i = 1; i <= k + 1; i++)
        ans = min(ans, dist[i * n]);
    printf("%d\n", ans);
    return 0;
}

本文由 落影汐雾 原创，采用 保留署名-非商业性使用-禁止演绎 4.0-国际许可协议
本文链接：https://x.lyxw.xyz/2019/layered_graph/

Powered by Hexo
Theme - Material