模板

最大流Dinic

没写当前弧优化什么的.

弃坑了，ISAP和HLPP有缘再学.

P3376 【模板】网络最大流

#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>

const int inf = 0x3fffffff;
const int N = 10005, M = 100005;
int n, m, s, t, maxflow;
int d[N];
struct Edge {
    int Nxt, v, flow;
}e[M << 1];
int h[N], p = 1;
void add(int u, int v, int z)
{
    e[++p].Nxt = h[u]; e[p].v = v; e[p].flow = z; h[u] = p;
    e[++p].Nxt = h[v]; e[p].v = u; e[p].flow = 0; h[v] = p;
}
std::queue<int> q;
bool bfs()
{
    memset(d, 0, sizeof(d));
    while(!q.empty()) q.pop();
    q.push(s); d[s] = 1;
    while(!q.empty())
    {
        int u = q.front(); q.pop();
        for(int i = h[u]; i; i = e[i].Nxt)
            if(e[i].flow && !d[e[i].v])
        {
            q.push(e[i].v);
            d[e[i].v] = d[u] + 1;
            if(e[i].v == t) return true;
        }
    }
    return false;
}
int dinic(int u, int flow)
{
    if(u == t) return flow;
    int rest = flow, k;
    for(int i = h[u]; i && rest; i = e[i].Nxt)
        if(e[i].flow && d[e[i].v] == d[u] + 1)
    {
        k = dinic(e[i].v, std::min(rest, e[i].flow));
        if(!k) d[e[i].v] = 0;
        e[i].flow -= k;
        e[i ^ 1].flow += k;
        rest -= k;
    }
    return flow - rest;
}
int main()
{
    scanf("%d%d%d%d", &n, &m, &s, &t);
    for(int i = 1, u, v, z; i <= m; i++) {
        scanf("%d%d%d", &u, &v, &z);
        add(u, v, z);
    }
    int flow = 0;
    while(bfs())
        while(flow = dinic(s, inf)) maxflow += flow;
    printf("%d\n", maxflow);
    return 0;
}

费用流EK

P3381 【模板】最小费用最大流

#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>

const int _ = 50005;
const int inf = 0x3f3f3f3f;
int n, m, s, t;
int ans, maxflow;
int dist[_], incf[_], pre[_], vis[_];
struct Edge { int Nxt, v, flow, cost; } e[_ << 1];
int h[_], p = 1;
void add(int u, int v, int f, int c)
{
    e[++p].Nxt = h[u]; e[p].v = v; e[p].flow = f; e[p].cost = c; h[u] = p;
    e[++p].Nxt = h[v]; e[p].v = u; e[p].flow = 0; e[p].cost = -c; h[v] = p;
}
std::queue<int> q;
bool spfa()
{
    memset(dist, 0x3f, sizeof(dist));
    memset(vis, 0, sizeof(vis));
    q.push(s); dist[s] = 0; vis[s] = 1;
    incf[s] = inf;
    while(!q.empty())
    {
        int u = q.front(); q.pop();
        vis[u] = 0;
        for(int i = h[u]; i; i = e[i].Nxt)
        {
            if(!e[i].flow) continue;
            int v = e[i].v;
            if(dist[v] > dist[u] + e[i].cost)
            {
                dist[v] = dist[u] + e[i].cost;
                incf[v] = std::min(incf[u], e[i].flow);
                pre[v] = i;
                if(!vis[v]) vis[v] = 1, q.push(v);
            }
        }
    }
    if(dist[t] == inf) return false;
    else return true;
}
void update()
{
    int u = t;
    while(u != s)
    {
        int i = pre[u];
        e[i].flow -= incf[t];
        e[i ^ 1].flow += incf[t];
        u = e[i ^ 1].v;
    }
    maxflow += incf[t];
    ans += dist[t] * incf[t];
}
int main()
{
    scanf("%d%d%d%d", &n, &m, &s, &t);
    for(int i = 1, u, v, z, c; i <= m; i++) {
        scanf("%d%d%d%d", &u, &v, &z, &c);
        add(u, v, z, c);
    }
    while(spfa()) update();
    printf("%d %d\n", maxflow, ans);
    return 0;
}

Problem

[NOI2008]志愿者招募

算法：线性规划 or ~~有源汇上下界最小费用可行流~~可以无视
一开始幻想这样可以搞：

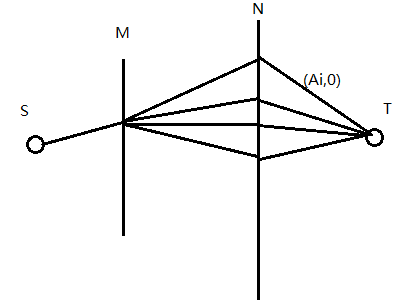
但其实很难限制条件并且流量并不能准确一对多去覆盖点。

所以是建成这样的：

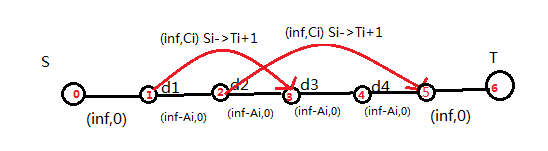
但是为什么对呢，其实非常玄学，我觉得还是手动模拟一下~~不会证~~，然后感性理解。

模拟时可以发现$inf-A[i]$其实对人数限制取反，代表要跑完这条边所有流量，流到$0$之前的流量是没有实际作用的，是为了可以先跳过这天，直到流量为$0$后，代表这条边需要开始选择人进行工作，而这条边需要的人数可以通过别的边反映出来，可以从红边即人补全这条链上为$0$的边无法通过的流量，通过最小费用最大流即可求出最小费用。

$n+1->t$这条边可以反映出当前还剩的未规划的最大人数，所以$n+1->t$流量为$0$时，代表之前最大流量流尽，即$(inf-A[i]){max}$，即$A[i]{min}$。

[NOI2012]美食节

从算法到算术，使用小学数学并利用大量算术技巧计算点的遍号

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define R register

using namespace std;
const int N = 45, M = 105, sP = 805, _ = N + M * sP + 5;
const int inf = 0x3f3f3f3f;
int n, m, s, t, sum, tim[N][M], P[N];
struct Edge { int Next, v, flow, cost; } e[(N + N * M * sP + M * sP + 5) << 1];
int h[N + M * sP + 5], p = 1;
inline void add(R int u, R int v, int f, int c) {
    e[++p].Next = h[u]; e[p].v = v; e[p].flow = f; e[p].cost = c; h[u] = p;
    e[++p].Next = h[v]; e[p].v = u; e[p].flow = 0; e[p].cost = -c; h[v] = p; 
}
int dist[_], incf[_], maxflow, ans, vis[_], pre[_];
queue<int> q;
bool spfa()
{
    memset(vis, 0, sizeof(vis));
    memset(dist, 0x3f, sizeof(dist));
    dist[s] = 0; vis[s] = 1; q.push(s); incf[s] = inf;
    while(!q.empty()) {
        int u = q.front(); q.pop();
        vis[u] = 0;
        for(int i = h[u]; i; i = e[i].Next)
            if(e[i].flow)
        {
            int v = e[i].v;
            if(dist[v] > dist[u] + e[i].cost) {
                dist[v] = dist[u] + e[i].cost;
                incf[v] = min(incf[u], e[i].flow);
                pre[v] = i;
                if(!vis[v]) q.push(v), vis[v] = 1;
            }
        }
    }
    if(dist[t] == inf) return false;
    else return true;
}
inline void update() {
    R int u = t;
    while(u != s) {
        int i = pre[u];
        e[i].flow -= incf[t];
        e[i ^ 1].flow += incf[t];
        u = e[i ^ 1].v;
    }
    maxflow += incf[t];
    ans += dist[t] * incf[t];
}
int main()
{
    scanf("%d%d", &n, &m);
    for(R int i = 1; i <= n; i++) scanf("%d", &P[i]), sum += P[i];
    s = 0, t = m * sum + n + 1;
    for(R int i = 1; i <= n; i++)
        for(R int j = 1; j <= m; j++)
            scanf("%d", &tim[i][j]);
    for(R int i = 1; i <= n; i++) add(s, i, P[i], 0);
    for(R int i = n + 1; i <= n + m * sum; i += sum) add(i, t, 1, 0);
    for(R int i = 1; i <= n; i++)
        for(R int j = n + 1, t = 1; j <= n + m * sum; j += sum)
            add(i, j, 1, tim[i][t++]);
    while(spfa()) {
        update();
        int u = e[pre[t] ^ 1].v;
        if((u - n) % sum == 0) break;
        int v = u + 1;
        int k = (v - n) % sum == 0 ? sum : (v - n) % sum;
        int j = (v - n - k) / sum + 1;
        add(v, t, 1, 0);
        for(R int i = 1; i <= n; i++)
            add(i, v, 1, k * tim[i][j]);
    }
    printf("%d\n", ans);
    return 0;
}

最大权闭合子图

参考资料：
——-1——-
——-2——-
——-3——-

定理最大权闭合子图权值=正权点之和-最小割

本文由落影汐雾原创，采用保留署名-非商业性使用-禁止演绎 4.0-国际许可协议
本文链接：https://x.lyxw.xyz/2019/network_flow/