「线段树」 | 落影汐雾的x号虚空印刷站

Update on A.D.2019-09-23

模板

struct Segment_Tree {
    #define ls (p << 1)
    #define rs (p << 1 | 1)
    #define mid ((l + r) >> 1)
    ll ans[_ << 2], tag[_ << 2];
    inline void pushup(ll p) { ans[p] = ans[ls] + ans[rs]; }
    inline void pushdown(ll p, ll l, ll r) {
        ans[ls] += (mid - l + 1) * tag[p];
        tag[ls] += tag[p];
        ans[rs] += (r - mid) * tag[p];
        tag[rs] += tag[p];
        tag[p] = 0;
    }
    void build(ll p, ll l, ll r) {
        if(l == r) {
            ans[p] = a[l];
            return;
        }
        build(ls, l, mid);
        build(rs, mid + 1, r);
        pushup(p);
    }
    void update(ll p, ll l, ll r, ll ul, ll ur, ll k) {
        if(ul <= l && r <= ur) {
            ans[p] += (r - l + 1) * k;
            tag[p] += k;
            return;
        }
        if(tag[p]) pushdown(p, l, r);
        if(ul <= mid) update(ls, l, mid, ul, ur, k);
        if(ur > mid) update(rs, mid + 1, r, ul, ur, k);
        pushup(p);
    }
    ll query(ll p, ll l, ll r, ll ql, ll qr) {
        if(ql <= l && r <= qr) return ans[p];
        if(tag[p]) pushdown(p, l, r);
        ll res = 0;
        if(ql <= mid) res += query(ls, l, mid, ql, qr);
        if(qr > mid) res += query(rs, mid + 1, r, ql, qr);
        return res;
    }
    #undef ls
    #undef rs
    #undef mid
}T;

题目

维护可加性变量解决问题

P3707 [SDOI2017]相关分析

$$\bar{x}=\frac{1}{R-L+1}\sum x_i​$$ $$\bar{y}=\frac{1}{R-L+1}\sum y_i$$ $$\hat{a}=\dfrac{\sum_{i=L}^R(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=L}^R(x_i-\bar{x})^2}$$

记$\sum = \sum_{i=L}^{R}​$

Query

$$Ans=\dfrac{ \sum x_iy_i-\bar{x}\sum y_i-\bar{y}\sum x_i+\sum \bar{x}\bar{y}}{\sum x_i^2-2\bar{x}\sum x_i+\sum\bar{x^2}}$$ $$=\dfrac{ \sum x_iy_i-\frac{1}{R-L+1}\sum x_i\sum y_i-\frac{1}{R-L+1}\sum y_i\sum x_i+\sum \frac{1}{R-L+1}\sum x_i\frac{1}{R-L+1}\sum y_i}{\sum x_i^2-\frac{1}{R-L+1}2\sum x_i\sum x_i+\sum (\frac{1}{R-L+1}\sum x_i)^2}$$ $$=\dfrac{ \sum x_iy_i-\frac{\sum x_i\sum y_i}{R-L+1}}{\sum x_i^2-\frac{(\sum x_i)^2}{R-L+1}}$$

下传Tag：先$upd$后$addX \quad addY$

维护值：$t1=\sum x$ | $t2=\sum y$ | $t3=\sum xy$ | $t4=\sum x^2$

维护Tag：$addX \quad addY$

$$\hat{a}=\dfrac{t3-\frac{t1t2}{R-L+1}}{t4-\frac{t1^2}{R-L+1}}$$

Add

$$\Delta x = S \quad \Delta y= T$$ $$\sum (x + S) = \sum x_i+(R-L+1)S$$ $$\sum(y+T)=\sum y_i+(R-L+1) T$$ $$\sum(x+S)(y+T)=\sum(xy+Sy+Tx+ST)=\sum xy+S\sum y+T\sum x+(R-L+1)ST$$ $$\sum(x+S)^2=\sum x^2+2S\sum x+(R-L+1)S^2$$

下传Tag：先$upd$后$addX \quad addY$

顺序：先$t3,t4$后$t1,t2$

Update

自然数平方和：$\sum_{i=1}^ni=\frac{n(n+1)(2n+1)}{6}$

1.$\forall i \in [L,R]\quad x_i=i\ \ y_i=i$

$$\sum x=\sum y = \sum i = \frac{(R-L+1)(R+L)}{2}$$ $$\sum x^2 = \sum xy = \sum i ^2 = \sum_{i=1}^R i^2-\sum_{i=1}^{L-1}i^2=\frac{R(R+1)(2R+1)}{6}-\frac{L(L-1)(2L-1)}{6}$$

下传Tag：先$upd$后$addX \quad addY$

清空Tag $addX \quad addY$

标记Tag $upd$

2.ADD L R S T

Code

#include <iostream>
#include <cstdio>
#define ll long long

using namespace std;
const int N = 100005;
int n, m;
double X[N], Y[N];
struct Segment_Tree
{
    #define ls (p << 1)
    #define rs (p << 1 | 1)
    #define mid ((l + r) >> 1)
    bool upd[N << 2];
    double x[N << 2], y[N << 2];
    double t1[N << 2], t2[N << 2], t3[N << 2], t4[N << 2];
    inline void pushup(ll p)
    {
        t1[p] = t1[ls] + t1[rs];
        t2[p] = t2[ls] + t2[rs];
        t3[p] = t3[ls] + t3[rs];
        t4[p] = t4[ls] + t4[rs];
    }
    inline void pushdown(ll p, ll l, ll r)
    {
        double L = mid - l + 1, R = r - mid;
        if(upd[p]) {
            double Ll = l, Lr = mid, Rl = mid + 1, Rr = r;
            t1[ls] = t2[ls] = (Lr - Ll + 1.0) * (Lr + Ll) / 2.0;
            t1[rs] = t2[rs] = (Rr - Rl + 1.0) * (Rr + Rl) / 2.0;
            t3[ls] = t4[ls] = Lr * (Lr + 1.0) * (2.0 * Lr + 1.0) / 6.0 - Ll * (Ll - 1.0) * (2.0 * Ll - 1.0) / 6.0;
            t3[rs] = t4[rs] = Rr * (Rr + 1.0) * (2.0 * Rr + 1.0) / 6.0 - Rl * (Rl - 1.0) * (2.0 * Rl - 1.0) / 6.0;
            upd[ls] = upd[rs] = upd[p]; upd[p] = 0;
            x[ls] = x[rs] = y[ls] = y[rs] = 0;
        }
        if(x[p] || y[p]) {
            t3[ls] += x[p] * t2[ls] + y[p] * t1[ls] + L * x[p] * y[p];
            t3[rs] += x[p] * t2[rs] + y[p] * t1[rs] + R * x[p] * y[p];
        }
        if(x[p]) {
            t4[ls] += 2 * x[p] * t1[ls] + L * x[p] * x[p];
            t4[rs] += 2 * x[p] * t1[rs] + R * x[p] * x[p];
            t1[ls] += L * x[p];
            t1[rs] += R * x[p];
            x[ls] += x[p];
            x[rs] += x[p];
            x[p] = 0;
        }
        if(y[p]) {
            t2[ls] += (double)L * y[p];
            t2[rs] += (double)R * y[p];
            y[ls] += y[p];
            y[rs] += y[p];
            y[p] = 0;
        }
    }
    void build(ll p, ll l, ll r)
    {
        if(l == r) {
            t1[p] = X[l];
            t2[p] = Y[l];
            t3[p] = X[l] * Y[l];
            t4[p] = X[l] * X[l];
            return;
        }
        upd[p] = x[p] = y[p] = 0;
        build(ls, l, mid);
        build(rs, mid + 1, r);
        pushup(p);
    }
    void add(ll p, ll l, ll r, ll ql, ll qr, double S, double T)
    {
        if(ql <= l && r <= qr) {
            double len = (r - l + 1);
            t3[p] += S * t2[p] + T * t1[p] + len * S * T;
            t4[p] += 2 * S * t1[p] + len * S * S;
            t1[p] += len * S;
            t2[p] += len * T;
            x[p] += S; y[p] += T;
            return;
        }
        pushdown(p, l, r);
        if(ql <= mid) add(ls, l, mid, ql, qr, S, T);
        if(qr > mid) add(rs, mid + 1, r, ql, qr, S, T);
        pushup(p);
    }
    void update(ll p, ll l, ll r, ll ql, ll qr) {
        if(ql <= l && r <= qr) {
            t1[p] = t2[p] = (double)(r - l + 1.0) * (l + r) / 2.0;
            t3[p] = t4[p] = (double)r * (r + 1.0) * (2.0 * r + 1) / 6.0 - (double)l * (l - 1.0) * (2.0 * l - 1.0) / 6.0;
            x[p] = y[p] = 0;
            upd[p] = 1;
            return;
        }
        pushdown(p, l, r);
        if(ql <= mid) update(ls, l, mid, ql, qr);
        if(qr > mid) update(rs, mid + 1, r, ql, qr);
        pushup(p);
    }
    double query(ll p, ll l, ll r, ll ql, ll qr, ll f) {
        if(ql <= l && r <= qr) {
            if(f == 1) return t1[p];
            if(f == 2) return t2[p];
            if(f == 3) return t3[p];
            if(f == 4) return t4[p];
        }
        pushdown(p, l, r);
        double res = 0;
        if(ql <= mid) res += query(ls, l, mid, ql, qr, f);
        if(qr > mid) res += query(rs, mid + 1, r, ql ,qr, f);
        return res;
    }
    #undef ls
    #undef rs
    #undef mid
};
struct Segment_Tree Tree;
int main()
{
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i++) scanf("%lf", &X[i]);
    for(int i = 1; i <= n; i++) scanf("%lf", &Y[i]);
    Tree.build(1, 1, n);
    int opt, L, R; double S, T;
    while(m--)
    {
        scanf("%d", &opt);
        if(opt == 1)
        {
            scanf("%d %d", &L, &R);
            double t1 = Tree.query(1, 1, n, L, R, 1);
            double t2 = Tree.query(1, 1, n, L, R, 2);
            double t3 = Tree.query(1, 1, n, L, R, 3);
            double t4 = Tree.query(1, 1, n, L, R, 4);
            double a_ = (t3 - (t1 * t2) / (double)(R - L + 1)) / (t4 - (t1 * t1) / (double)(R - L + 1));
            printf("%.10lf\n", a_);
        }
        else if(opt == 2)
        {
            scanf("%d %d %lf %lf", &L, &R, &S, &T);
            Tree.add(1, 1, n, L, R, S, T);
        }
        else if(opt == 3)
        {
            scanf("%d %d %lf %lf", &L, &R, &S, &T);
            Tree.update(1, 1, n, L, R);
            Tree.add(1, 1, n, L, R, S, T);
        }
    }
    return 0;
}

Tag的用法

区间01取反xor
区间翻转rev
区间最长连续1/0
区间min/max子段和
P2572 [SCOI2010]序列操作

扫描线

矩形面积并
P1502 窗口的星星
P1856 [USACO5.5]矩形周长Picture

二维线段树

树套树
P3437 [POI2006]TET-Tetris 3D

其它

Luogu P2061 [USACO07OPEN]城市的地平线City Horizon

简单题

算法

线段树 + 离散化

思路

对$(x,y,h)$的左右端点$x,y$进行离散化，离散化前的原值记为$val[i]$，对每个矩形按高度$h$从小到大排序。

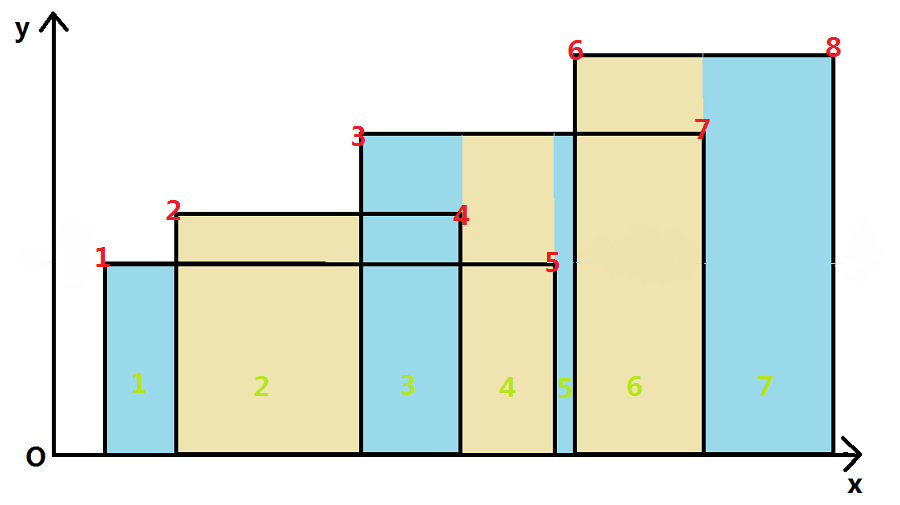
设离散化后的端点有$M$个，则对如图所示$M-1$个规则矩形编号为$[1,M-1]$，可以由$h_{[i, i+1]}\times(val[i+1] - val[i])$得出第$i$个矩形的面积。

开一颗区间为$[1,M-1]$的线段树，按$h$从小到大依次对线段树区间覆盖，可以保证高的矩形覆盖了低的矩形的区间，具体操作为对离散化后的$(x,y,h)$，进行线段树$[x,y-1]$区间覆盖$h$值，最终$i$点存储$h_{[i,i+1]}$的最大值。

$h_{[i, i+1]}$可以通过线段树单点查询$i$点求出。

答案：$\sum{i=1}^{M-1}h{[i, i+1]}\times(val[i+1] - val[i])$

代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#define ll long long

using namespace std;
const int N = 80005;
int n, b[N], val[N];//b[]:离散化数组
struct Line { int x, y, h; }a[N];//存储每个矩形
bool cmp(Line a, Line b) { return a.h < b.h; }
int ans[N << 2];//线段树数组
#define ls (p << 1)
#define rs (p << 1 | 1)
#define mid ((l + r) >> 1)
void update(int p, int l, int r, int ul, int ur, int k)
{
    if(ul <= l && r <= ur) { ans[p] = k; return; }
    if(ans[p]) ans[ls] = ans[rs] = ans[p], ans[p] = 0;//区间覆盖直接下推
    if(ul <= mid) update(ls, l, mid, ul, ur, k);
    if(ur > mid) update(rs, mid + 1, r, ul, ur, k);
}
ll query(int p, int l, int r, int x)//单点查询
{
    if(l == r) return ans[p];
    if(ans[p]) ans[ls] = ans[rs] = ans[p], ans[p] = 0;//区间覆盖直接下推
    if(x <= mid) return query(ls, l, mid, x);
    if(x > mid) return query(rs, mid + 1, r, x);
}
#undef ls
#undef rs
#undef mid
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].h);
        b[i] = a[i].x; b[n + i] = a[i].y;//离散化数组记录下所有x,y
    }
    sort(b + 1, b + 2 * n + 1);//排序
    int _n = unique(b + 1, b + 2 * n + 1) - (b + 1);//去重，_n为去重后x,y端点个数
    for(int i = 1; i <= n; i++)
        if(a[i].x != a[i].y)//x=y没有作用
    {
        int x = a[i].x, y = a[i].y;
        a[i].x = lower_bound(b + 1, b + _n + 1, a[i].x) - b;
        a[i].y = lower_bound(b + 1, b + _n + 1, a[i].y) - b;//离散化
        val[a[i].x] = x; val[a[i].y] = y;//原值
    }
    sort(a + 1, a + n + 1, cmp);//按h从小到大排序
    for(int i = 1; i <= n; i++)
        if(a[i].x != a[i].y)//防止y-1<x
            update(1, 1, _n - 1, a[i].x, a[i].y - 1, a[i].h);//更新,注意结点个数是_n-1，端点y要变成矩形区域y-1，可以画图理解一下，相当于把端点x右边的矩形区域编号为x
    ll res = 0;
    for(int i = 1; i < _n; i++)
        res += query(1, 1, _n - 1, i) * (val[i + 1] - val[i]);
    printf("%lld\n", res);
    return 0;
}

本文由 落影汐雾 原创，采用 保留署名-非商业性使用-禁止演绎 4.0-国际许可协议
本文链接：https://x.lyxw.xyz/2019/segment_tree/